문제
n×n 바둑판 모양으로 총 n2개의 방이 있다. 일부분은 검은 방이고 나머지는 모두 흰 방이다. 검은 방은 사면이 벽으로 싸여 있어 들어갈 수 없다. 서로 붙어 있는 두 개의 흰 방 사이에는 문이 있어서 지나다닐 수 있다. 윗줄 맨 왼쪽 방은 시작방으로서 항상 흰 방이고, 아랫줄 맨 오른쪽 방은 끝방으로서 역시 흰 방이다.
시작방에서 출발하여 길을 찾아서 끝방으로 가는 것이 목적인데, 아래 그림의 경우에는 시작방에서 끝 방으로 갈 수가 없다. 부득이 검은 방 몇 개를 흰 방으로 바꾸어야 하는데 되도록 적은 수의 방의 색을 바꾸고 싶다.
아래 그림은 n=8인 경우의 한 예이다.
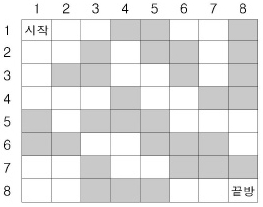
위 그림에서는 두 개의 검은 방(예를 들어 (4,4)의 방과 (7,8)의 방)을 흰 방으로 바꾸면, 시작방에서 끝방으로 갈 수 있지만, 어느 검은 방 하나만을 흰 방으로 바꾸어서는 불가능하다. 검은 방에서 흰 방으로 바꾸어야 할 최소의 수를 구하는 프로그램을 작성하시오.
단, 검은 방을 하나도 흰방으로 바꾸지 않아도 되는 경우는 0이 답이다.
입력
첫 줄에는 한 줄에 들어가는 방의 수 n(1 ≤ n ≤ 50)이 주어지고, 다음 n개의 줄의 각 줄마다 0과 1이 이루어진 길이가 n인 수열이 주어진다. 0은 검은 방, 1은 흰 방을 나타낸다.
출력
첫 줄에 흰 방으로 바꾸어야 할 최소의 검은 방의 수를 출력한다.
bfs를 이용해서 출발지점에서 각 지점까지의 최소 접근 거리를 구하면 됩니다.
방문배열 v에 거리를 저장합니다.
#include<bits/stdc++.h>
#define FAST ios_base::sync_with_stdio(false),cin.tie(NULL);
#define mset(v) memset(v,0,sizeof(v));
#define rep(i,a) for(int i=0;i<a;++i)
#define REP(i,a) for(int i=1;i<=a;++i)
using namespace std;
typedef long long ll;
typedef pair<int, int> pi;
typedef tuple<int, int, int>ti;
typedef vector<int> vi;
typedef vector<vector<int>> vvi;
int dy[4] = { -1,0,1,0 }, dx[4] = { 0,1,0,-1 };
int N, MAX = 987654321;
int a[51][51], v[51][51];
int main() {
FAST;
cin >> N;
char x;
REP(i, N) {
REP(j, N) {
cin >> x;
a[i][j] = (x - '0');
v[i][j] = MAX;
}
}
queue<pi>q;
q.push({ 1,1 });
v[1][1] = 0;
while (!q.empty()) {
auto top = q.front();
q.pop();
int y = top.first;
int x = top.second;
rep(i, 4) {
int ny = y + dy[i];
int nx = x + dx[i];
if (a[ny][nx] == 1 && v[ny][nx]>v[y][x]) {
v[ny][nx] = v[y][x];
q.push({ ny,nx });
}
else if (a[ny][nx] == 0 && v[ny][nx] > v[y][x] + 1) {
v[ny][nx] = v[y][x] + 1;
q.push({ ny,nx });
}
}
}
cout << v[N][N];
}'baekjoon' 카테고리의 다른 글
| [백준] 10942 팰린드롬? (1) | 2024.03.25 |
|---|---|
| [백준] 10159 저울 (0) | 2024.03.21 |
| [백준] 2457 키 순서 (0) | 2024.03.21 |
| [백준] 4256 트리 (0) | 2024.03.21 |
| [백준] 17829 222-풀링 (0) | 2024.03.21 |