문제
그래프가 주어졌을 때, 단절선을 모두 구해 출력하는 프로그램을 작성하시오.
단절선이란 그 간선을 제거했을 때, 그래프가 두 개 또는 그 이상으로 나누어지는 간선을 말한다. 즉, 제거했을 때 그래프의 connected component의 개수가 증가하는 간선을 말한다.
입력
첫째 줄에 두 정수 V(1≤V≤100,000), E(1≤E≤1,000,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B가 주어진다. 이는 A번 정점과 B번 정점이 연결되어 있다는 의미이며, 방향은 양방향이다.
그래프는 항상 연결되어 있으며, 같은 간선이 두 번 이상 들어오는 경우는 없다. 또, A와 B가 같은 경우도 없다.
그래프의 정점은 1부터 V까지 자연수이다.
출력
첫째 줄에 단절선의 개수 K를 출력한다.
둘째 줄부터 K개 줄에는 단절선을 사전순으로 한 줄에 하나씩 출력한다. 간선은 "A B" 형식으로 출력해야 하고, A < B를 만족해야 한다. 같은 간선은 한 번만 출력하면 된다. 즉, "A B"를 출력한 경우에 "B A"는 출력할 필요가 없다.
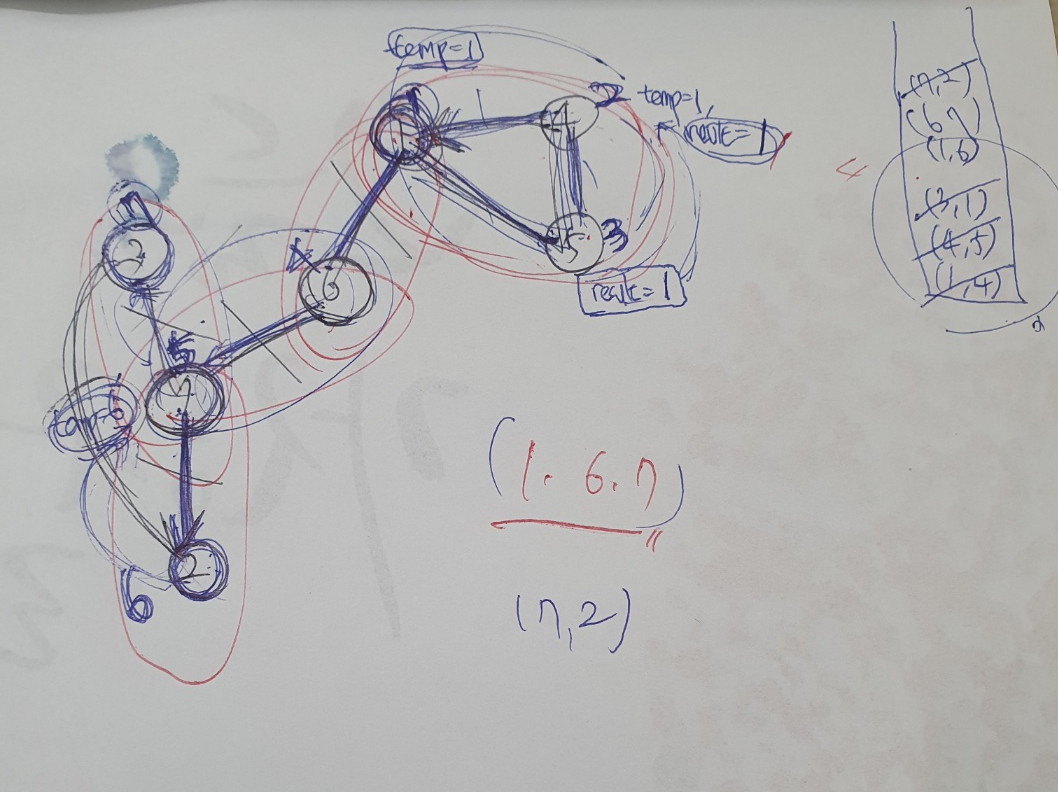
자식노드의 dfsn과 현재노드의 dfsn을 비교할때, 만약 자식노드가 현재노드의 dfsn과 같지 않고, 더 크다면
현재노드를 발견하여 싸이클이 발생한게 아니라, 더이상 올라갈 노드가 없다는 의미이므로 그 간선은 단절선입니다.
#include<bits/stdc++.h>
#define FAST ios_base::sync_with_stdio(false),cin.tie(NULL);
#define mset(v) memset(v,0,sizeof(v));
#define rep(i,a) for(int i=0;i<a;++i)
#define REP(i,a) for(int i=1;i<=a;++i)
using namespace std;
typedef long long ll;
typedef pair<int, int> pi;
typedef tuple<int, int, int>ti;
typedef vector<int> vi;
typedef vector<vector<int>> vvi;
int dy[] = { -1,0,1,0 }, dx[] = { 0,1,0,-1 }, INF = 987654321;
int V, E, dfsn[1000001], cnt;
stack<pi>st;
vi adj[1000001];
vvi bcc;
vector<pi>bc;
//pre는 부모노드를 의미합니다.
int dfs(int k,int pre=-1) {
//result는 도달가능한 정점의 최소 dfsn을 저장합니다.
int result = dfsn[k] = ++cnt;
//모든 도달가능한 정점에대해
for (int next : adj[k]) {
//부모노드라면 생략
if (next == pre)continue;
//만약 처음 방문하는 간선이라면 stack에 Push
if (dfsn[k] > dfsn[next])st.push(pi{ k,next });
//이미 방문한 정점이라면, dfsn값을 비교하여 result에 작은값을 저장합니다
if (dfsn[next] > 0)result = min(result, dfsn[next]);
//처음 방문한 정점이라면 dfs로 진행합니다
else {
//result와 자식정점의 dfsn와 비교해 작은값을 저장합니다.
int temp = dfs(next, k);
result = min(result, temp);
//만약 현재 dfsn과 자식 dfsn을 비교했을때, 현재값이 크거나 같으면
//현재노드의 부모노드로는 더이상 갈 수 없음을 의미합니다. BCC를 발견했습니다.
//현재노드까지 BCC입니다.
if (temp >= dfsn[k]) {
if (temp > dfsn[k]) {
// 해당 간선은 단절선입니다
pi top = st.top();
pi d;
st.pop();
if (top.first > top.second) {
d = { top.second,top.first };
}
else {
d = { top.first,top.second };
}
bc.push_back(d);
}
else {
vi vt;
while (!st.empty()) {
pi top = st.top();
st.pop();
vt.push_back(top.first);
vt.push_back(top.second);
if (top == pi{ k,next })break;
}
bcc.push_back(vt);
}
}
}
}
return result;
}
int main() {
FAST;
cin >> V >> E;
while (E--) {
int a, b;
cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
rep(i, V) {
if (dfsn[i] == 0) {
dfs(i);
}
}
cout << bc.size() << "\n";
sort(bc.begin(), bc.end());
for (auto R : bc) {
cout << R.first << " " << R.second << "\n";
}
}
'baekjoon' 카테고리의 다른 글
| [백준] 6672 Electricity (0) | 2023.07.04 |
|---|---|
| [백준] 10891 Cactus? Not cactus? -선인장그래프 (0) | 2023.07.03 |
| [백준] 11266 단절점 + BCC 이중 연결 요소 (0) | 2023.07.03 |
| [백준]11689 GCD(n,k) - 오일러 파이 함수 (0) | 2023.07.03 |
| [백준] 17086 아기 상어 2 (0) | 2023.06.29 |