문제
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으며, 각 지점 사이의 이동은 지도에서 상하좌우 이웃한 곳끼리만 가능하다.
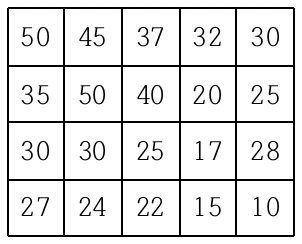
현재 제일 왼쪽 위 칸이 나타내는 지점에 있는 세준이는 제일 오른쪽 아래 칸이 나타내는 지점으로 가려고 한다. 그런데 가능한 힘을 적게 들이고 싶어 항상 높이가 더 낮은 지점으로만 이동하여 목표 지점까지 가고자 한다. 위와 같은 지도에서는 다음과 같은 세 가지 경로가 가능하다.
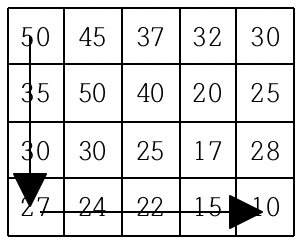
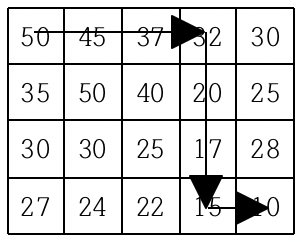
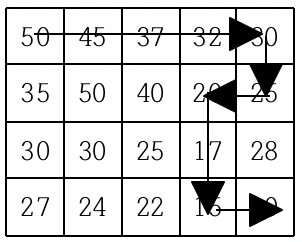
지도가 주어질 때 이와 같이 제일 왼쪽 위 지점에서 출발하여 제일 오른쪽 아래 지점까지 항상 내리막길로만 이동하는 경로의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 지도의 세로의 크기 M과 가로의 크기 N이 빈칸을 사이에 두고 주어진다. 이어 다음 M개 줄에 걸쳐 한 줄에 N개씩 위에서부터 차례로 각 지점의 높이가 빈 칸을 사이에 두고 주어진다. M과 N은 각각 500이하의 자연수이고, 각 지점의 높이는 10000이하의 자연수이다.
출력
첫째 줄에 이동 가능한 경로의 수 H를 출력한다. 모든 입력에 대하여 H는 10억 이하의 음이 아닌 정수이다.
골3 DP+DFS 문제입니다
처음에 간단하게 DFS로만 푸는데 시간초과가 나왔습니다. 따라서 DP를 이용해서 방문처리와 동시에 이미 존재하는 길이 있는지 확인해주어야 합니다
visited는 미방문상태에서 -1로 초기화해주고, 방문하면 0으로 만들어줍니다.
한 점A 에서 이동할 수 있는 목적지까지 가는 경우의 수는 A의 상,하,좌,우 점에서 목적지까지 가는 경우의 수의 합과 같다.
도착지에서 거리가 1인 점에서 목적지로 가능 경우의 수는 1이므로, 위의 규칙을 계속해서 따라간다면
한번 방문한 visited 좌표는 다시 방문해 업데이트할 필요가 없습니다.
#include<bits/stdc++.h>
using namespace std;
int n, m;
int mp[501][501];
int visited[501][501];
int dy[4] = { -1,0,1,0 };
int dx[4] = { 0,1,0,-1 };
int dfs(int y, int x) {
if (y == n - 1 && x == m - 1) { //기저
return 1;
}
if (visited[y][x] != -1) //만약 이미 방문했다면 업데이트할 필요가 없습니다
//저장되어있는 값이 곧 목적지로 가는 경우의 수이므로 그대로 반환해줍니다.
return visited[y][x];
visited[y][x] = 0;
for (int i = 0; i < 4; i++) {
if (y + dy[i] >= 0 && y + dy[i] < n && x + dx[i] >= 0 && x + dx[i] < m) {
if (mp[y][x] > mp[y + dy[i]][x + dx[i]]) {
visited[y][x] += dfs(y + dy[i], x + dx[i]); //상하좌우에서 목적지로가는 경우의 수를 모두 더합니다.
}
}
}
return visited[y][x];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
memset(mp, 0, sizeof(mp));
memset(visited, -1, sizeof(visited));
int x;
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> x;
mp[i][j] = x;
}
}
cout << dfs(0, 0);
}============================================================================================
욕심쟁이 판다문제와 같은 결의 문제입니다.
이미 한번 방문했던 요소에 대해서는 또다시 방문할 필요가 없습니다! 따라서 메모제이션을 사용합니다.
이때 주의할점!
#include<bits/stdc++.h>
#define FAST ios_base::sync_with_stdio(false);cin.tie(NULL)
#define mset(v) memset(v,0,sizeof(v));
#define rep(i,a) for(int i=0;i<a;++i)
#define REP(i,a) for(int i=1;i<=a;++i)
using namespace std;
typedef long long ll;
typedef pair<int, int> pi;
typedef tuple<int, int, int>ti;
typedef vector<int> vi;
typedef vector<vector<int>> vvi;
int dy[] = { -1,0,1,0 }, dx[] = { 0,1,0,-1 };
int N, M, mp[501][501], v[501][501], ans = -1;
int dfs(int y, int x) {
if (v[y][x])return v[y][x];
if (y == N - 1 && x == M - 1)return 1;
rep(i,4) {
int ny = y + dy[i];
int nx = x + dx[i];
if (ny >= 0 && ny < N && nx >= 0 && nx<M && mp[y][x]>mp[ny][nx]) {
v[y][x] += dfs(ny,nx);
}
}
return v[y][x];
}
int main() {
FAST;
cin >> N >> M;
rep(i, N)rep(j, M) cin >> mp[i][j];
dfs(0, 0);
cout << v[0][0];
}위 처럼 코드를 작성하면 시간초과가 발생합니다.
이유는....
만약 어떤 정점K에서 더이상 움직이는 경우가 없으면 0을반환해야합니다.
그런데 배열 v를 0으로 초기화 시켜놨기 때문에, 이미 방문한 정점인지 확인할 길이 없습니다.
따라서 시간초과가 발생합니다.
이를 막기위해 배열 v를 -1로 초기화 시키면 됩니다.
#include<bits/stdc++.h>
#define FAST ios_base::sync_with_stdio(false);cin.tie(NULL)
#define mset(v) memset(v,0,sizeof(v));
#define rep(i,a) for(int i=0;i<a;++i)
#define REP(i,a) for(int i=1;i<=a;++i)
using namespace std;
typedef long long ll;
typedef pair<int, int> pi;
typedef tuple<int, int, int>ti;
typedef vector<int> vi;
typedef vector<vector<int>> vvi;
int dy[] = { -1,0,1,0 }, dx[] = { 0,1,0,-1 };
int N, M, mp[501][501], v[501][501], ans = -1;
int dfs(int y, int x) {
if (v[y][x]!=-1)return v[y][x];
if (y == N - 1 && x == M - 1)return 1;
v[y][x] = 0;
rep(i,4) {
int ny = y + dy[i];
int nx = x + dx[i];
if (ny >= 0 && ny < N && nx >= 0 && nx<M && mp[y][x] > mp[ny][nx]) {
v[y][x] += dfs(ny,nx);
}
}
return v[y][x];
}
int main() {
FAST;
cin >> N >> M;
memset(v, -1, sizeof(v));
rep(i, N)rep(j, M) cin >> mp[i][j];
dfs(0, 0);
cout << v[0][0];
}
작년엔 간신히 풀었는데 이번에 다시풀땐 금방풀어서 기분이 좋습니다 ㅎㅎ
'baekjoon' 카테고리의 다른 글
| [백준] 10999 구간 합 구하기2 + 느리게 갱신되는 세그먼트 트리 (0) | 2023.02.14 |
|---|---|
| [백준] 11505 구간 곱 구하기 (복습) (0) | 2023.02.13 |
| [백준] 1937. 욕심쟁이 판다 + 복습 (0) | 2023.02.13 |
| [백준] 1108 검색 엔진 + Unordered_map 해쉬맵으로 사용 (0) | 2023.02.09 |
| [백준] 9470 Strahler 순서 (0) | 2023.02.08 |