문제
방향 그래프가 주어졌을 때, 그 그래프를 SCC들로 나누는 프로그램을 작성하시오.
방향 그래프의 SCC는 우선 정점의 최대 부분집합이며, 그 부분집합에 들어있는 서로 다른 임의의 두 정점 u, v에 대해서 u에서 v로 가는 경로와 v에서 u로 가는 경로가 모두 존재하는 경우를 말한다.
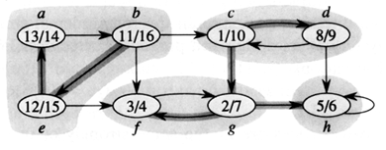
예를 들어 위와 같은 그림을 보자. 이 그래프에서 SCC들은 {a, b, e}, {c, d}, {f, g}, {h} 가 있다. 물론 h에서 h로 가는 간선이 없는 경우에도 {h}는 SCC를 이룬다.
입력
첫째 줄에 두 정수 V(1 ≤ V ≤ 10,000), E(1 ≤ E ≤ 100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B가 주어진다. 이는 A번 정점과 B번 정점이 연결되어 있다는 의미이다. 이때 방향은 A → B가 된다.
정점은 1부터 V까지 번호가 매겨져 있다.
출력
첫째 줄에 SCC의 개수 K를 출력한다. 다음 K개의 줄에는 각 줄에 하나의 SCC에 속한 정점의 번호를 출력한다. 각 줄의 끝에는 -1을 출력하여 그 줄의 끝을 나타낸다. 각각의 SCC를 출력할 때 그 안에 속한 정점들은 오름차순으로 출력한다. 또한 여러 개의 SCC에 대해서는 그 안에 속해있는 가장 작은 정점의 정점 번호 순으로 출력한다.
유향 그래프에서 두 정점 u,v가 있을 때, u에서 v로 가는길, 그리고 v에서 u로 가는길이 있으면 u v 는 같은 scc에 속해있습니다.
따라서 유향 그래프가 있을때, SCC는 사이클과 연관되어있습니다.
#include<bits/stdc++.h>
using namespace std;
int V, E, A, B;
vector<int> adj[10001];
vector<vector<int>>scc;
int num = 0, v[10001], s[10001], cnt = 0;
vector<int>st;
int dfs(int k) {
st.push_back(k); //스택을 사용합니다.
int parent = v[k] = ++num; //parent; 부모값(방문처리)초기화>>자기자신의 번호
for (auto c : adj[k]) { //모든 엣지에 대해 O(E)
if (!v[c]) { //미방문시
parent = min(parent, dfs(c)); //parent를 자기자신의 번호와, dfs(c)중 작은 값으로
//Union Find와 비슷한 맥락으로 부모노드의 인덱스를 저장해놓습니다
}
else if (!s[c]) { //이미 방문한 지점인데 scc가 아니면 scc입니다.
parent = min(parent, v[c]); //parent 값과 v[child]값을 비교해서 작은걸 저장합니다.
}
//방문했는데 scc면 그대로 진행합니다.
}
//이후 만약 저장한 parent값이 자신의 부모값과 동일하다면, 그 지점을 기준으로 scc를 돕니다.
if (parent == v[k]) {
cnt++; //scc 갯수 ++
vector<int>temp;
while (1) {
auto t = st.back(); //스택에서 k가 나올 때 까지 scc에 저장할겁니다
st.pop_back();
s[t] = cnt;
temp.push_back(t);
if (k == t)break;
}
sort(temp.begin(), temp.end());
scc.push_back(temp);
}
return parent; //재귀를 통해 저장한 parent값을 모든 scc 내부의 정점에대해 부모값을 통일시킵니다.
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cin >> V >> E;
for (int i = 0; i < E; i++) {
cin >> A >> B;
adj[A].push_back(B);
}
for (int i = 1; i <= V; i++) { //All DFS 모든 정점에 대해 dfs 를 수행합니다. O(V)
if (!v[i])
dfs(i);
}
sort(scc.begin(), scc.end());
cout << cnt << "\n";
for (int i = 0; i <scc.size(); i++) {
for (int j = 0; j < scc[i].size(); j++) {
cout << scc[i][j] << " ";
}
cout << "-1\n";
}
}우선 타잔 알고리즘에서 사용하는 변수로는
배열 v : 방문처리와 , 부모노드인덱스를 저장합니다.
배열 s : scc에 속해있는지 확인합니다.
스텍 st: BFS를 스택으로 수행하고 , SCC(사이클)을 발견하는 경우 뽑아냅니다.
'baekjoon' 카테고리의 다른 글
| [백준] 11281 2-SAT -4 (0) | 2023.01.20 |
|---|---|
| [백준] 11280 2-SAT-3 (0) | 2023.01.19 |
| [백준]11377 열혈강호 3,11378 열혈강호 4 (0) | 2023.01.17 |
| [백준] 1671. 상어의 저녁식사 + 벡터에 값을 입력하는 빠른 방법 (0) | 2023.01.17 |
| [백준] 1348 주차장. (0) | 2023.01.11 |