[백준] 11111 두부장수 장홍준2

문제

장홍준은 참 특이한 두부장수이다. 세로크기 N, 가로크기 M인 두부판을 가지고 2x1짜리 두부로 잘라서 판다. 그런데, 두부판의 위치마다 등급이 다르다. 그리고 2x1짜리에 등급이 어떻게 매겨지느냐에 따라 두부의 값도 천차만별이 된다. 다음 등급표를 보자.

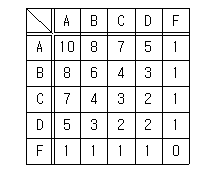
위의 표는 2x1짜리 두부의 등급에 따라 매겨지는 두부의 가격표다. 예를 들어 “AC" 두부의 가격은 7이고, ”DB" 두부의 가격은 3이다.

세로크기 M, 가로크기 N의 두부판이 주어진다. 각 칸마다 두부의 등급이 A, B, C, D, F로 매겨져 있다. 홍준이는 전체 두부가격의 합을 최대가 되게 두부를 자르려고 한다. 2x1짜리 두부로 잘라내고 남은 한 칸짜리 두부는 가격이 0이기 때문에 버린다. 홍준이를 도와 가격이 최대가 되게 두부판을 자르는 프로그램을 작성하시오.

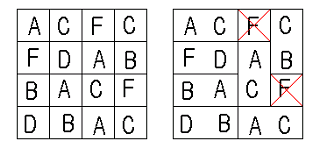
위 그림은 N=4, M=4 인 두부판의 한 예이다. 오른쪽 그림이 잘라낸 두부가격의 합을 최대로 한 것이다. 한 칸짜리는 쓸모없으므로 버린다.

입력

첫째 줄에는 두부판의 세로크기 N, 가로크기 M이 주어진다. N, M은 1이상 50이하의 정수이다. 그 다음 N줄에 걸쳐 M개의 문자가 주어진다. 각 문자는 그 칸의 두부의 등급을 나타내며 A, B, C, D, F 중 하나로 주어진다.

출력

첫째 줄에 잘라낸 두부가격 합의 최댓값을 출력한다.

 

체스판격자무늬처럼, 한정점과 다음정점을 번갈아가면서 A그룹과 B그룹으로 나눕니다.

A그룹 하나와 B그룹 하나를 묶어 간선 하나로 연결할 수 있습니다. capacity는 1입니다. 즉, 2*1 짜리 두부로 잘라낸다는 의미입니다.

 

이런식으로 모델링을 하고, 각 간선당 cost를 정하면

MCMF문제로 풀 수 있습니다

SPFA를 사용합니다.

 

다만 중요한 점은, 이 MCMF문제에서는 매칭이 늘어난다고해서 최대 가격이 늘어나는게 아닙니다. 

매칭을 늘리더라도 최대가격이 줄어들 수 도 있기때문에, 최대가격이 늘어나는선까지만 SPFA를 수행해야합니다.

#include<bits/stdc++.h>
#define FAST ios_base::sync_with_stdio(false),cin.tie(NULL);
#define mset(v) memset(v,0,sizeof(v));
#define rep(i,a) for(int i=0;i<a;++i)
#define REP(i,a) for(int i=1;i<=a;++i)

using namespace std;

typedef long long ll;
typedef pair<int, int> pi;
typedef tuple<int, int, int>ti;
typedef vector<int> vi;
typedef vector<vector<int>> vvi;
int dy[] = { -1,0,1,0 }, dx[] = { 0,1,0,-1 }, INF = 987654321;

using namespace std;
int N, M, S = 2501, E = 2502, c[2503][2503], f[2503][2503], idx[2503][2503], cost[2503][2503], A, B = 1250, ans;
//1~1800,1251~2500,3601,3602
vi score[6], adj[2503];
char mp[51][51];
int main() {
	FAST;
	score[0] = { 10,8,7,5,0,1 };
	score[1] = { 8,6,4,3,0,1 };
	score[2] = { 7,4,3,2,0,1 };
	score[3] = { 5,3,2,2,0,1 };
	score[4] = { 0,0,0,0,0,0 };
	score[5] = { 1,1,1,1,0,0 };
	cin >> N >> M;
	REP(i, N)REP(j, M) {
		cin >> mp[i][j];
		if ((i + j) % 2 == 0) {
			idx[i][j] = ++A;
		}
		else idx[i][j] = ++B;
	}
	REP(i, N)REP(j, M) {
		if ((i + j) % 2 == 0) {
			c[S][idx[i][j]] = 1;
			adj[S].push_back(idx[i][j]);
			adj[idx[i][j]].push_back(S);
			rep(k, 4) {
				int ny = i + dy[k];
				int nx = j + dx[k];
				if (ny >= 1 && ny <= N && nx >= 1 && nx <= M) {
					adj[idx[i][j]].push_back(idx[ny][nx]);
					adj[idx[ny][nx]].push_back(idx[i][j]);
					c[idx[i][j]][idx[ny][nx]] = 1;

					cost[idx[i][j]][idx[ny][nx]] = - score[mp[i][j] - 'A'][mp[ny][nx] - 'A'];
					cost[idx[ny][nx]][idx[i][j]] = score[mp[i][j] - 'A'][mp[ny][nx] - 'A'];
				}
			}
		}
		else {
			c[idx[i][j]][E] = 1;
			adj[idx[i][j]].push_back(E);
			adj[E].push_back(idx[i][j]);
		}
	}
	while (1) {
		queue<int>q;
		q.push(S);
		int p[2503], dist[2503], inQ[2503];
		fill(p, p + 2503, -1);
		fill(dist, dist + 2503, INF);
		mset(inQ);
		inQ[S] = 1;
		dist[S] = 0;
		while (!q.empty()) {
			int cur = q.front();
			inQ[cur] = 0;
			q.pop();
			for (int nxt : adj[cur]) {
				if (c[cur][nxt] - f[cur][nxt] > 0 && dist[nxt] > dist[cur] + cost[cur][nxt]) {
					dist[nxt] = dist[cur] + cost[cur][nxt];
					p[nxt] = cur;
					if (!inQ[nxt]) {
						inQ[nxt] = 1;
						q.push(nxt);
					}
				}
			}
		}
		if (p[E] == -1)break;
		int temp = 0;
		for (int i = E; i != S; i = p[i]) {
			temp -= cost[p[i]][i];
			f[p[i]][i] += 1;
			f[i][p[i]] -= 1;
		}
		if (temp > 0)ans += temp;
		else break;
	}
	cout << ans;
}