[백준] 4013 ATM
문제
인도의 도시 중 하나인 시루세리에는 모든 도로들이 일방통행으로 되어 있다. 도로들이 만나는 모든 교차로에는 시루세리 은행의 현금입출금기(ATM)가 설치되어 있다. 시루세리에는 유명한 레스토랑 체인인 아웃백 커리 하우스가 있다. 이 레스토랑의 각 체인점들은 교차로에만 위치한다. 물론 각 교차로마다 항상 이 레스토랑 체인점이 있는 것은 아니다. 이 레스토랑은 현금만 사용할 수 있다.
시루세리에 사는 반디치는 오늘 오후에 이 레스토랑에서 가족들과 파티를 열려고 한다. 그런데 갖고 있는 현금이 부족하여 레스토랑으로 가는 동안에 가능한 한 많은 현금을 ATM 기기로부터 인출할 계획을 세웠다. 그는 자신의 집에서 출발하여 차로 이동하면서 통과하는 모든 교차로 ATM 기기에 들어있는 현금 전부를 인출하려고 한다. 차량의 최종 목적지는 아웃백 커리 하우스 체인점 중의 한 곳이고, 이 체인점이 어떤 교차로에 위치하는지는 상관없다.
반디치는 시루세리 은행의 홈페이지 정보를 통해 각 ATM 기기에 현금이 얼마나 들어 있는지를 알고 있다. 이동 시 동일한 도로나 교차로를 여러 번 지날 수 있다. ATM 기기의 현금은 새로 보충되지 않기 때문에 첫 번째 이후 다시 방문하는 교차로의 ATM 기기에는 인출할 현금이 없다.
예를 들어, 아래 그림처럼 도시에 6개의 교차로가 있다고 하자. 교차로는 원으로 표시되어 있고, 화살표는 도로를 나타낸다. 이중 원으로 표시된 교차로에는 레스토랑이 있다. 각 ATM 기기가 갖고 있는 현금의 액수는 교차로 위에 표시된 숫자이다. 이 예에서 현금 인출을 1번 교차로부터 시작한다면, 반디치는 1-2-4-1-2-3-5의 경로를 통해서 총 47의 현금을 인출할 수 있다.
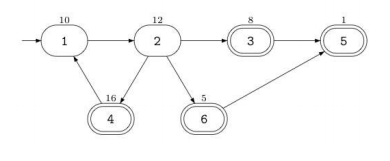
반디치가 출발 장소에서 어떤 레스토랑까지 이동하면서 인출할 수 있는 현금의 최대 액수가 얼마인지를 계산하는 프로그램을 작성하시오.
입력
첫째 줄에 교차로의 수와 도로의 수를 나타내는 2개의 정수 N과 M(N, M ≤ 500,000)이 차례로 주어진다. 교차로는 1부터 N까지 번호로 표시된다. 그 다음 M개의 줄에는 각 줄마다 각 도로의 시작 교차로 번호와 끝 교차로 번호를 나타내는 2개의 정수가 주어진다. 그 다음 N개의 줄에는 1번 교차로부터 차례대로 각 교차로의 ATM 기기가 보유한 현금의 액수를 나타내는 정수가 각 줄에 하나씩 주어진다. 그 다음 줄에는 두 개의 정수 S와 P가 주어진다. 여기서 S는 출발 장소(현금 인출의 시작 장소)인 교차로 번호이고 P는 레스토랑의 개수이다(1 ≤ P ≤ N). 그 다음 줄에는 각 레스토랑이 있는 교차로의 번호를 나열한 P개의 정수가 주어진다.
각 ATM 기기에 들어 있는 현금의 액수는 0 이상 4,000 이하이다. 모든 입력에서 경로의 출발 장소로부터 일방통행 도로를 통해 도달 가능한 레스토랑이 항상 하나 이상 존재한다.
출력
출력은 한 개의 정수이다. 이 정수는 반디치가 출발 장소에서 어떤 레스토랑까지 이동하면서 인출할 수 있는 현금의 최대 액수이다.
반디치가 도로를 다니면서 가능한 한 많은 돈을 뽑아 식당에 도착해야합니다.
도로는 여러번 다닐 수 있습니다.
따라서, 도로가 사이클을 형성한다면, 그 도로의 교차로에있는 ATM기에서는 모든 돈을 뽑을 수 있습니다.
마찬가지로 한 사이클 위에 한 교차로에만 식당이 존재하면, 사이클에 도착하기만 하면 식당에 갈 수 있습니다.
따라서 도로를 scc로 구성된 단방향그래프로 옮겨 지도를 새로 그린다면 , 도달할 수 있는 모든 scc에 대해 뽑을 수 있는 돈을 저장하고, 식당에 도착했는지 확인만하면 됩니다.
scc로 구분하기위해 타잔알고리즘을 사용하고,
scc기준으로 인접리스트를 작성합니다.
#include<bits/stdc++.h>
using namespace std;
int N, M, S, P, ATM[500001], money[500001], rest[500001], v[500001], s[500001], num = 0, cnt = 0, dp[500001], ans = 0;
vector<int>adj[500001], st, adjs[500001];
int dfs(int k) {
st.push_back(k);
int parent = v[k] = ++cnt;
for (auto r : adj[k]) {
if (!v[r])
parent = min(parent, dfs(r));
else if (!s[r])
parent = min(parent, v[r]);
}
if (parent == v[k]) {
num++;
vector<int>temp;
while (1) {
auto r = st.back(); st.pop_back();
temp.push_back(r);
s[r] = num;
if (r == k)break;
}
}
return parent;
}
void tarjan() {
for (int i = 1; i <= N; i++)
if (!v[i])dfs(i);
}
int dfs2(int k) {
if (dp[k]!=-1)return dp[k]; //이미 존재하면 출력
for (auto r : adjs[k]) {
auto c = dfs2(r);
if (c != -1)
//만약 이전 scc에 식당이 있는경우 dp값 갱신 가능
dp[k] = max(dp[k], money[k] + c);
else if (rest[k])
//이전 scc에 대해 식당은 없지만 현재 scc에 식당이 있다면 갱신가능
dp[k] = max(dp[k], money[k]);
}
//리프scc일때, 식당이 있다면 갱신
if (dp[k]==-1) dp[k] = rest[k] ? money[k] : -1;
return dp[k];
}
int main() {
cin >> N >> M;
int x, y;
while (M--) {
cin >> x >> y;
adj[x].push_back(y);
}
for (int i = 1; i <= N; i++)
cin >> ATM[i];
cin >> S >> P;
tarjan(); //타잔 알고리즘
while (P--) {
cin >> x;
for (int i = 1; i <= N; i++)
rest[s[x]] = 1; //scc에 식당이 존재하는지 저장
}
for (int i = 1; i <= N; i++) {
money[s[i]] += ATM[i]; //scc내부 ATM기에서 뽑을 수 있는 돈을 저장
for (auto r : adj[i])
if (s[i] != s[r])
adjs[s[i]].push_back(s[r]); //scc으로 만든새로운 인접리스트
}
for (int i = 1; i <= num; i++) {
sort(adjs[i].begin(), adjs[i].end());
adjs[i].erase(unique(adjs[i].begin(), adjs[i].end()), adjs[i].end());
}//인접리스트 중복제거
memset(dp, -1, sizeof(dp));
cout<<dfs2(s[S]); //DP를 이용해 답 출력
}
마지막 답을 출력할때 DP를 사용해야 합니다.....
단방향이기 때문에 dp사용가능합니다.